محاسبه سینوس و معکوس آن
مثلثات
از نامگذاری مثلثات میتوان حدس زد که این شاخه از ریاضیات دست کم در آغاز پیدایش خود به نحوی با “مثلث“ و مساله های مربوط به مثلث ارتباط داشته است. در واقع پیدایش و پیشرفت مثلثات را باید نتیجهای از تلاشهای ریاضی دانان در جهت رفع دشواریهای مربوط به محاسبههایی دانست که در هندسه و در اخترشناسی رو به روی دانشمندان بوده است. در ضمن دشواریهای هندسی، خود ناشی از مساله هایی بوده است که دانشمندان در اخترشناسی با آن رو به رو میشده اند و بیشتر جنبهی محاسباتی داشتهاند.
پس احتمالاً مثلثات برای استفاده از ستاره شناسی (اخترشناسی) ایجاد شده و کاربردهای اولیه آن نیز در همین باره بوده است. در اخترشناسی اغلب به مساله هایی برخورد میکنیم که برای حل آنها به مثلثات و دستورهای آن نیازمندیم.سادهترین این مسائل، پیدا کردن یک کمان دایره (برحسب درجه) است، وقتی که شعاع دایره و طول وتر این کمان معلوم باشد یا برعکس،
پیدا کردن طول وتری که طول شعاع دایره و اندازه کمان آن معلوم باشد. کهنترین جداولی که از دانشمندان قدیمی به جای مانده است، متعلق به اخترشناسان و ریاضی دانان سدهی دوم میلادی است و شاید بتوان این جداول را نخستین گام در پیدایش مثلثات دانست ولی همهی کارهای این ریاضی دانان و اخترشناسان که یونانی بودهاند، در درون هندسه انجام گرفت و هرگز به مفهومهای اصلی مثلثات نرسیدهاند.
دانشمندان جهان
نخستین گامهای اصلی به وسیلهی آریابهاتا ریاضی دان هندی سدهی پنجم میلادی برداشته شد که در واقع تعریفی برای نیم وتر یک کمان داد. از این به بعد به تقریب همه کارهای مربوط به شکل گیری مثلثات (چه در روی صفحه و چه در روی کره) به وسیلهی دانشمندان ایرانی انجام گرفت.خوارزمی نخستین جدولهای سینوسی را تنظیم کرد و پس از او همهی ریاضی دانان ایرانی گامهایی در جهت تکمیل جدولها و گسترش مفهومهای مثلثاتی برداشتند. احمدابن عبدالله حبش حاسب جدول سینوسها را تقریباً ٣٠ درجه به ٣٠ درجه تنظیم کرد و برای گسترش و برای نخستین بار به دلیل نیازهای اخترشناسی مفهوم “ تانژانت “ را تعریف کرد.
دانشمندان ایرانی
جدیترین تلاشها به وسیله ی ابوریحان بیرونی و ابوالوفای بوزجانی انجام گرفت که توانستند مثلثات را تا جایی پیش ببرند که مثلث کروی را هم حل کنند. ابوالوفا با روش جالبی به یاری نابرابریها توانست مقدار سینوس کمان ٣٠ دقیقه را پیدا کنند و سرانجام خواجه نصیرالدین طوسی با جمع بندی کارهای دانشمندان ایرانی پیش از خود، نخستین کتاب مستقل مثلثات را نوشت. بعد از طوسی جمشید کاشانی ریاضی دان ایرانی زمان تیموریان با روش زیبایی که برای حل معادلهی درجه سوم پیدا کرده بود، توانست راهی برای محاسبهی کمان یک درجه با هر دقت دلخواه پیدا کند. پیشرفت بعدی دانش مثلثات از سدهی پانزدهم میلادی و در اروپای غربی انجام گرفت.
یک نمونه از مواردی که ایرانی بودن این دانش را نشان میدهد از این قرار است: ریاضی دانان ایرانی برای سینوس از واژهی «جیب» و برای کسینوس از واژهی «جیب تمام» استفاده میکردند. وقتی نوشتههای ریاضی دانان به ویژه خوارزمی به زبان لاتین و زبان اروپایی ترجمه شد، معنای واژهی جیب را در زبان خود به جای آن گذاشتند سینوس. این کلمه در لاتین همان معنای جیب را در عربی دارد.
دایره مثلثاتی
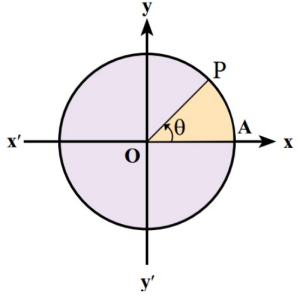
پرسشی که بهطور طبیعی به ذهن میرسد این است که نسبتهای مثلثاتی در مورد زوایای غیرحاده تعریف میشود؟ مثلاً برای زاویه ١۵٠ درجه میتوان سینوس تعریف کرد و چگونه؟ جواب مثبت است. اما مثلث قائم الزاویه دیگر جوابگوی این تعریف نیست. دایره مثلثاتی را برای این منظور معرفی میکنیم.دایرهای به شعاع یک و مرکز مبداء مختصات. اگر از نقطه (٠, ١)A و در خلاف جهت حرکت عقربههای ساعت شروع به حرکت کنیم زاویهای مثبت تولید خواهد شد. در صورت چرخش در جهت عقربههای ساعت زاویهی منفی حاصل میشود.
روابط بین نسبت های مثلثاتی
شاید تا الان متوجه شده باشید که چهار نسبت مثلثاتی علیرغم نام های متفاوت با هم ارتباط نزدیکی دارند. این روابط را در زیر فهرست کرده ایم :
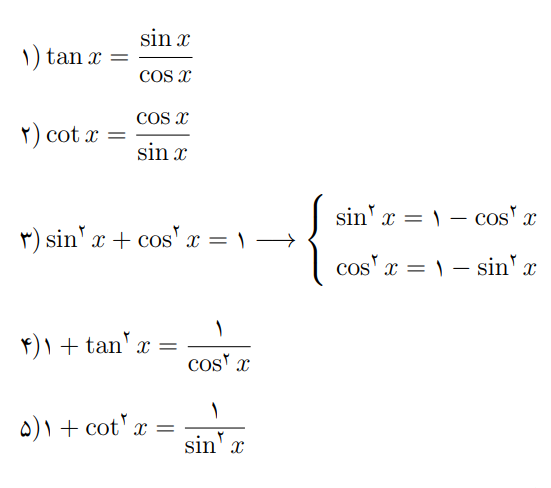
ابزار آنلاین محاسبه سینوس و معکوس آن
ابزار آنلاین بالا به راحتی و در کوتاهترین زمان ممکن مقدار سینوس و معکوس آنرا را با توجه به دادههای شما محاسبه میکند. فقط کافی است مقدار زاویه مورد نظر و کمیت آنرا انتخاب کنید و دکمه محاسبه کن را فشار دهید.
